Регулирование коэффициента трансформации автотрансформаторов связи под нагрузкой обычно осуществляется переключением ответвлений со стороны вывода среднего напряжения. При этом коэффициент трансформации между обмотками ВН и НН не изменяется. Второй случай подключения БК приведен на рис. 28,6. Здесь присоединение осуществляется к шинам распределительных сетей. Трансформатор, как правило, имеет регулирование под нагрузкой.

fOHHi

Рис. 28. Схемы включения конденсаторных батарей системного значения. а - включение БК на обмотку среднего напряжения автотрансформатора связи; б - Bi-слючение БК на шины вторичного напряжения подстанции с трансформаторами, имеющими РПН.

Для выяснения вопроса о принципах управления режимом БК системного значения необходимо рассмотреть более общий вопрос о принципах автоматического управления режимами электрических сетей в целом. Этот вопрос тем более актуален в связи с внедрением автоматизированных систем управления энергетикой.

Математическая модель автоматически регулируемого режима электрической системы представляет собой сложную функцию многих схемных и режимных параметров. Оптимизация режима осуществляется в результате поиска минимума функционала издержек на электроснабжение по всем влияющим параметрам с учетом различных ограничений.

В процессе широкого внедрения вычислительной техники и кибернетических методов управления в центре внимания специалистов встали сейчас организационно-

экономические предпосылки применения электронно-вычислительных и информационных систем. Речь идет об установлении оптимальных соотношений между централизацией в управлении, о выявлении объективно необходимого объема и характера информации на разных ступенях иерархического управления энергосистемами, о разработке рациональной структуры использования ЦВМ. Для этой цели целесообразно выявлять внутреннюю логику процесса, устанавливать взаимосвязи между явлениями. Использование этих взаимосвязей в дальнейшем может в ряде случаев упростить решение задач управления производственным процессом в энергосистемах. К подобным задачам, в частности, относится управление электрическими системами.

Оптимизационные расчеты режимов электрических систем обычно проводятся в несколько этапов. Для решения вопросов, связанных с автоматизацией осуществления оптимальных режимов, необходимо иметь результаты оптимизационных расчетов, включающие определение как уровней напряжения, так и распределения реактивных нагрузок.

На основе периодически получаемой информации о нагрузках электрической системы на ЦВМ можно получить достаточно большое число оптимизационных расчетов. Далее рассматриваются оптимальные параметры режима для отдельных узлов электрической системы. Предполагается также, что регулирование режимов сетей различных напряжений осуществляется независимо из-за наличия регулирующих устройств в точках их примыкания. Оптимизируемыми параметрами режима узлов системы следу(т считать напряжение и реактивные составляющие токов элементов электрической системы, отходящих от узла (один из токов является зависимым). По числу оптимизируемых параметров режима для каждого узла можно построить систему координат. Комплекс оптимальных параметров узла, соответствующий оптимальному режиму электрической системы в целом, может быть изображен точкой в этой системе координат. Точки, соответствующие всему комплексу оптимизационных расчетов, которые охватывают режимы некоторого периода времени, заполняют определенное пространство параметров режима. Будем его называть пространством оптимальных параметров (ОП). При наличии двух параметров это пространство является дву-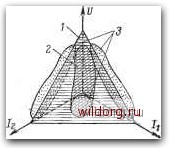

мерным, т. е. представляет собой плоскость. Для трех параметров пространство будет трехмерным, а для п параметров - соответственно п-мерным. Представление о форме пространства ОП может иметь важное практическое значение. Оказывается, что это пространство охватывает некоторую гиперплоскость в пространстве

i- координат режима узла, определенным образом ориентированную в нем. На рис. 29 в качестве примера изо-

, бражена фигура этого пространства в трехмерной систе-

Рис. 29. Пространство оптимальных параметров режима узла электрической сети.

/ - плоскость, соответствующая уравнению настройки регулятора; 2 - область плоскости, соответствующая реальным параметрам режима; 3 - проекции пространства оптимальных параметров режимов на плоскостях системы координат.

ме координат параметров режима узла. Очевидно, что основные соотношения между оптимальными параметрами режимов узла электрической системы следует оценивать по точкам внутри сечения, образованного некоторой плоскостью, секущей пространство ОП в продольном направлении и расположенной в нем по правилу наименьших квадратов. Несовпадение точек, характеризующих оптимальный режим, с точками этой плоскости в пространстве ОП характеризует некоторое рассеивание параметров в области оптимальных значений. Точкам упомянутого сечения соответствует уравнение, которое может быть записано в виде

f/i=f/o -f ,/eVii -f... + kJin +AI (29)

и решается в виде

/«=r2-f. . .-{-knIin-kiUi + U\

где Ui - напряжение узла в им режиме; Ли ..., kn - неизвестные постоянные параметры, которые в дальнейщем будут называться регрессионными коэффициентами; гь ..., 1гп - оптимальные значения реактивных составляющих токов узла для i-ro режима; А/ - ошибка, которая оценивается как вероятностная; Uo - постоянная величина, представляющая собой свободный член уравнения регрессии.