заведомо будет меньше I. Таким образом, получаем оценку ИР,)<-. (4.3)

В теории регулирования время переходного процесса часто называют временем регулирования.

Как первая, так и вторая теоремы Ляпунова имеют про-

стой геометрический смысл. Неравенство й = Xi<0

i = \

означает, что траектории системы (4.1) направлены в сторону убывания функции v, т. е. пересекают поверхности уровня этой функции в направлении, противоположном направлению вектора gradt;.

§ 5. Теорема об асимптотической устойчивости

Рассмотрим сначала некоторые предельные свойства траекторий.

Определение 5.1. Точка фазового пространства называется ш-предельной точкой точки р, если существует последовагельность моментов времени {t„}, t„ - co при и -со, такая, что q = =\im f{p, t). Если же -

со, тоточка q=\ixaf(p,tn)

называется 7.-педе ль ной. точкой точки р. Так, например, асимптотически устойчивое положение равновесия является (о-предельной точ--кой для всех точек, лежащих в достаточно мало* окрестности этого положения. Точки предельного цикла, на который навиваются спиралевидные кривые (рис. 2), Рис. 2. также, являются ш-предель-

ными для точек, принадлежащих этим кривым. В обоих примерах ш-предельные точки составляют целые траектории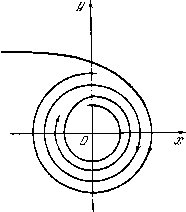

(в первом случае - особая точка, во втором - предельный цикл). Этот факт не случаен. Имеет место следующее утверждение.

Теорема 5.1. Множество ш-предельных ((х-предельных) точек данной точки есть замкнутое множество, состоящее из целых траекторий.

Прежде всего заметим, что замкнутость множества ш-пре-дельных точек есть следствие одной известной теоремы из теории множеств. Эта теорема утверждает, что предельная точка для предельных точек множества снова является предельной точкой этого множества. Допустим теперь, что точка q является ш-предельной точкой для точки р, и покажем, что точка f{q, х) (число х может иметь как положительный, , так и отрицательный знак) также является ш-предельной для точки р. В самом деле, если q-limf(p, t„), то из группо-

вого свойства динамических систем (см. § 1) и свойства непрерывности f{p, t) как функции р, получим f{q, х) = = lim-f-х), а это и означает, что точка f{q,x) явля-

ется (о-предельной точкой точки р, т. е. все точки траектории, выходящей из q, являются ш-предельными точками для р.

Множество, состоящее из целых траекторий, часто называют инвариантным множеством. Инвариантное множество А обладает тем свойством, что f{A, t)=A при любом t. Если же f{A, t)CiA при tO, то множество А назовем положительно инвариантным.

Заметим, что если траектория f{p, t) не выходит при fto из ограниченной части пространства, то множество ее (о-предельных точек не пусто.

Лемма 5.1. Если существует функция Ляпунова v, ограниченная снизу (сверху) в положительно инвариантной области D, и если производная по времени ii этой функции знакоотрицательна (знакоположительна) в этой области, то все т-предельные точки данной точки р лежат на одной и той же поверхности уровня функции v.

В самом деле, пусть точка р лежит в области D и пусть точка q = \in\f(p,t, является ш-предельной для р. Прежде

Л->00

всего заметим, что функция v(f(p,t)) при i -со не возрастает и ограничена снизу, следовательно, существует предел

S 51 ТВОРВМА ОБ АСИМПТОТИЧЁСкОЙ УСТОЙЧИВОСТИ 25

v„ = \\mv(f{p, t)). в силу непрерывности функции v имеем

t-*co

также v{q) = \imv(f{p, tn)), но так как v{f{p,t)) монотонно

п->оо

меняется, то имеем, очевидно, v{q) = v, что и доказывает лемму.

Теорема 5.2. Если существует определенно положительная функция V такая, ято v<0 вне М м »О на М, где М - множество, не содержащее целых траекторий, кроме точки О, то положение равновесия О асимптотически устойчиво.

Докажем теорему. Очевидно, положение равновесия - точка О устойчиво в смысле Ляпунова, так как выполняются условия теоремы 4.1. В силу устойчивости существует для заданного положительного числа е положительное число 5 такое, что если р CZ Л- то f(p, t) CZ Л при

Так как траектория f{p, t) не выходит при за пре-

делы шара то множество Q ш-предельных точек точки р не пусто. Если Q совпадает с точкой О, то теорема доказана, так как будем иметь \Ы/(р,1) = 0.

Допустим, что множество Q содержит по крайней мере одну точку q, отличную от точки О. Из леммы 5.1 следует, что

v{q) = v if{q, 0) = lim v {f{p, t)) ф 0.

/->00

Таким образом, все ш-предельные точки р лежат на одной и той же поверхности уровня v=-v{q). Из теоремы 5.1 следует, что множество Q замкнуто и состоит из целых траекторий. Таким образом, lan как v вдоль этих траекторий остается постоянной, то имеем tii=0 на всем множестве Q. По условию теоремы множество Q должно содержаться в множестве М, но множество М не содержит целых траекторий. Полученное противоречие доказывает теорему.

Заметим, что из теоремы 5.2 следует справедливость теоремы 4.2, таким образом, теорема 5.2 является усилением теоремы Ляпунова об асимптотической устойчивости. Теорема 5.2 позволяет решить вопрос об асимптотической устойчивости с помощью функции Ляпунова, имеющей знакопостоянную производную. В конкретных примерах именно такие функции Ляпунова удается чаще всего построить для