§ 3 ФУНКЦИИ ЛЯПУНОВА 17

переходит, таким образом, в задачу устойчивости нулевого решения х = 0 системы (2.3).

Сформулируем теперь определение устойчивости нулевого решения х = 0 системы (2.3).

Решение х=:0 системы (2.3) называется устойчивым в смысле Ляпунова, если для любого положительного числа s можно указать положительное число 8 такое, что из неравенства 1(о)11<С следует при ft неравенство х(0<С- Если же, кроме того, всякое решение x(t), начальные данные которого определяются условием х(о) <, обладает свойством Иш х(0=0. то нулевое решение

/ сю

называется асимптотически устойчивым в смысле Ляпунова. Аналогично вводятся понятия равномерной асимптотической устойчивости и устойчивости в целом.

§ 3. Функции Ляпунова

Рассмотрим функцию v (Xi, ..., х„), определенную в фазовом пространстве переменных Xi, ..., х„, непрерывную в некоторой области Д включающей в себя начало координат. Предположим также, что функция v (Xi, ..., х„) обладает в области D непрерывными частными производными.

Функцию v(Xi..... х„) назовем определенно положительной в области D, если всюду в области D, кроме точки О (О, ..., 0), имеет место неравенство г» 0. Если же выполняется неравенство v<0, то функция v называется определенно отрицательной. В том и другом случае функция может называться также знакоопределенной.

Если в области D имеет место всюду неравенство или неравенство fsgO, то функция v называется знакопостоянной, причем в первом случае функция v может быть также названа знакоположительной, а во втором - знако-отрицательной.

Если функция V принимает в области D значения как положительного знака, так и отрицательного, то в этом случае V называют знакопеременной функцией. Например, функция v = x\-\-xl - Хз будет знакопеременной функцией в пространстве переменных Xi, Xj, Хз, а функция t» = Xj-J--- Xj + Хз - определенно положительной в этом пространстве. Функция t» = Xj--X2 будет, однако, знакопосюянной в

пространстве переменных Xj, Xj, Xj (так как она обращается в нуль на оси Охз) и знакоопределенной в пространстве переменных X,, Xj.

Чаще всего мы будем иметь дело только с квадратичными формами переменных х„ ..., х„. Очевидно, любую квадратичную форму можно записать в виде

S a-ikXiXk, где а.-Аа*.. Составим матрицу коэффициентов этой формы:

и рассмотрим определители

а,! ... а,

й*1 • • • й** .

k=\, 2, п.

Если имеют место неравенства О при k-\, 2, ..., я, то форма V будет определенно положительной.

Справедлива и обратная теорема, т. е. условия ДО, называемые критерием Сильвестра [5], являются необходи-MHiMH и достаточными для определенной положительности формы V. Из критерия Сильвестра легко выводится необходимое и достаточное условие определенной отрицательности формы V. Это условие записывается в виде неравенств

Д,<0, Д.>0, Дз<0.....

т. е. определители Д должны последовательно чередовать знак, причем знак Д] должен быть отрицательным.

В дальнейщем мы будем изучать поведение функции V (Xi, ..., х„) вдоль траекторий изучаемой системы дифференциальных уравнений, и на основании этого изучения будем делать вывод о поведении траекторий рассматриваемой системы. Функции V (Xi, ..., х„), имеющие указанное сейчас назначение, принято теперь называть функциями Ляпунова.

Сформулируем теорему о структуре поверхности уровня знакоопределенной функции Ляпунова.

Теорема 3.1. Если функция v{Xi, дг„) знакооп-ределенна, то существует такое положительное число h, что все поверхности уровня v = с, где \ c\<h, являются замкнутыми относительно точки О поверхностями.

Заметим, что мы называем поверхность v = c замкнутой относительно точки О, если на любой непрерывной линии, соединяющей точку О с точкой границы области D, имеется по крайней мере одна точка, в которой v - c.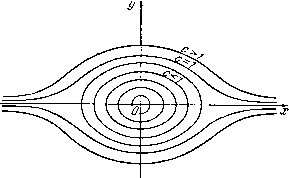

Рис. 1.

Для доказательства теоремы предположим для определенности и рассмотрим шар Jj с центром в начале координат и радиусом, равным R. Предположим, что функция v определена на этом шаре (включая его границу S/). Таким образом, в качестве области D мы возьмем шар Jj = 7дJ Sj. Так как функция v непрерывна, то на замкнутом ограниченном множестве S[p границе шара, эта функция достигает своего минимального значения, которое обозначим через ft.

Соединим теперь точку О с какой-либо точкой р, лежащей на границе некоторой непрерывной линией x = x{s). Так как в точке О функция v равна нулю, а v(p)h, и так как функция v меняется непрерывно вдоль непрерывной кривой x = x{s), то функция V необходимо в некоторой точке этой кривой примет значение v = c.

Таким образом, внутри шара лежит замкнутая часть поверхности v = c; не исключается возможность, что другие части этой поверхности расположены за предела!йи этого