ТО все точки поверхности 5 будут завершать свое движение к началу координат вдоль прямой (11.15).

Если наряду с (11.16) выполнено неравенство fi - 4А<0, то «второе скольжение» не будет иметь места. В этом случае изображающая точка, попав, например, на часть 5з, доходит до линии 0Q. Если К - достаточно большая величина, то линия OQi целиком далее переходит в линию OQj, лежащую как угодно близко к линии OQ4. В самом деле, след плоскости Dy-{-z = Q на плоскости 7 = 0 лежит в этом случае вне сектора, образованного следами плоскостей = 0, = 0. В области 7, 0, >• О, х О действует неустойчивая система, так как а=- 1. Величина 7 вдоль траектории движения не меняет знак. Поэтому при К достаточно большом переход точки М с линии OQ, на линию 0Q, можно считать совершающимся по некоторой прямой.

Попав на линию OQi, изображающая точка М будет скользить по части до тех пор, пока не дойдет до сектора прошиваемости L\OLi. Попав на линию OZ-i, изображающая точка сойдет с поверхности 5 и через малый промежуток времени (сравнить с § 7) снова попадет на поверхность 5, но уже на часть S.

Заметим, что если бы проекция точки М на плоскости (x, v) двигалась в силу системы (11.7), то за время она попала бы на линию D\X y = Q (с точностью до малых «(Л" )). Этот факт подсказывает следующую интерпретацию движения по поверхности 5: поверхность /? = 0 непрерывна, R - Ri{x,y,z) и знак А меняется не на плоскости 7=0, а на плоскости 7 = DiX-}-y = 0.

Если пренебречь в этом случае ошибкой одинакового порядка с АГ, то движение точки по поверхности 5 можно описать системой

х=у, р= - By - а,Лх, а, = sign X (j;--DjX). (11.17)

Производная по времени функции v= Ах-\-у, взятая в силу системы (11.17), имеет вид

г>= -2вУ + 2А(1 -ац)ху =

- 2ву при (DiX--;;)xO,

- 2Ву-4А\ху\ при (D,x + y)x<0.

Следовательно, функция v{x,y) удовлетворяет условиям

теоремы 12.2 первой главы, из которой следует асимптотическая устойчивость в целом нулевого решения системы (11.17). Впрочем, справедливость нашей теоремы в данном случае вытекает из непосредственного качественного исследования поведения траекторий на поверхности 5. Заметим, ЧТО в этом случае изображающая точка движется к точке О по спиралевидной кривой, отклоняющейся незначительно ОТ 5 в секторах LiOL, LOL.

Заметим, наконец, что доказанную теорему можно было бы трактовать как теорему об асимптотической устойчивости нулевого положения равновесия. Ради математической строгости л-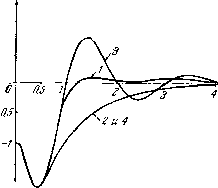

S t(ce/()

Рис. 17.

можно было бы в этом случае показать, что для любого еО можно указать число 8 такое, что из Хо--j(/o--2„"<8 следовало бы при О x{t) +У(0 + {1) е, где х {t\ y{t), z{t) - решение системы (П.2), определяемое начальными условиями X (0) = х„, у (0) = у„, Z (0) = Zq.

Однако доказательство этого факта мы опускаем, заметим только, что это доказательство можно было бы провести точно так же, как это сделано в § 8 второй главы.

На рис. 17 приводятся графики переходных процессов, полученные на модели МН-14, при следующих значениях параметров: а = 0, ft-O, с=1, К=\00. Кривая (1) соответствует значениям параметров А=12, В = 2, D= 2,34. Очевидно, в эгом случае выполняются оба неравенства (11.6). Кривая (2) соответствует случаю, когда выполняются нера-

венства (ИЛЗ) и (11.14); здесь принято А=10, В=10, D = 5. Кривая (4) совпадает с кривой (2), так как она получена при Л =10, В =10, D=20. Изменение D обеспечило в этом случае выполнение неравенств (11.13) и (11 16), однако не отразилось на протекании переходного процесса, что вполне соответствует выводам, приведенным выше, так как в обоих рассмотренных случаях движение завершается вдоль прямой (11.15).

Наконец, кривая (3) соответствует значениям Л=10, В=2, D=10. В этом случае выполнены неравенства В - - 4Л<0 и (11.16), следовательно, скольжение второго порядка отсутствует.

Таким образом, только переходный процесс, изображенный кривой (1), соответствует процессу с наличием скольжения второго порядка. Из сравнения указанных кривых следует вывод о значительных преимуществах систем переменной структуры с форсированным скользящим режимом.