Рассмотрим функцию Ляпунова

v = s.Jy - 2\cf(x, 0)dx. (8.13)

Из условия с) следует, что функция v является определенно положительной и бесконечно большой.

Вычислив производную V в силу системы (8.12), получим

v = 2y[cf{x, y)-cf{x, 0)]-2\s\[K\x\.\-Ki\y\-\r --A:2s + cp(x, y)\]-{-2s[ - F{x, y, s-j-cp(x, y))-<fy--

- cp;(s+cp(x, у))-\У].

Принимая во внимание условия а), Ь), получим

v2y[cfix,y)-<f{x, 0)]-2 \s\[iK~a)\x\.(Ki-

-b-M-l)3,+(/C,-c-A01s + cp(x, ;;)].

Так как, по условиям теоремы, выполняются соотношения с) и (8.11), то из последнего неравенства следует, что производная функции V, взятая в силу системы (8.12), будет знакоотрицательной функцией, обращающейся в нуль на оси Ох. Очевидно, на оси Ох нет целых траекторий системы (8.2), за исключением особой точки 0(0, О, 0); кроме того, функция V является бесконечно большой. Таким образом, можно применить теперь теорему (12.2) первой главы, что и заканчивает доказательство нашей теоремы.

Что касается соображений относительно качественного расположения траекторий системы (8.9), то легко видеть, что поверхность Z= ср(х, у) является поверхностью скольжения во всех ее точках. Это проверяется вычислениями, подобными тем, которые проведены в доказательстве теоремы 8.1. Поэтому изображающая точка системы (8.9) при f -> оо либо непосредственно приближается асимптотически к началу координат, либо попадает предварительно через конечное время на поверхность скольжения, а затем, двигаясь по ней, также асимптотически приближается к началу координат.

§ 9. Исследование системы третьего порядка с разрывной поверхностью переключения

Рассмотрим уравнение третьего порядка

х-{-ах-Ьх-сх= -я-Кх, (9.1)

эквивалентное системе

х=у, р = г,=-сх - by - az - аКх. (9.2)

Предположим, что параметры а, Ь, с, К являются произвольными постоянными, причем коэффициент К-положителен.

Рассмотрим сначала за-I /\ \ дачу отыскания закона

Y \ \. изменения а при усло-

X ВИИ I а 1 £ 1, обеспечи-

вающего максимальное

относительное быстродействие системы, т. е. попадание точек фазового пространства в достаточно малую окрестность начала координат за минимальное время.

Анализ этой задачи приводит к необходимости вводить сложный закон переключения величины а; этот закон необходимо должен быть нелинейным, так как одна из поверхностей переключения должна быть необходимо нелинейной, хотя и содержащей в качестве своей части плоские многообразия. Учитывая, что нелинейный закон переключения является трудно реализуемым, можно искать решение на пути построения кусочно линейной поверхности переключения, такой, чтобы при движении точки фазового пространства по ней происходило изменение режима скольжения с целью повышения быстродействия.

Детальный анализ оптимальных задач приводит к мысли построения поверхности переключения из двух плоскостей. Такая поверхность (рис. 14), в отличие от поверхности, рассмотренной нами ранее, имеет разрыв на плоскости х=0 и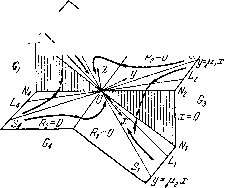

Рис. 14.

обеспечивает, в некотором смысле, первое приближение решения указанной выше оптимальной задачи.

Здесь ставится, однако, задача не оптимизации системы (9.2), а задача стабилизации системы. Это значит, что за счет упрощения структуры поверхности переключения переходный процесс, описываемый системой (9.2), будет несколько отличаться от оптимального. Необходимо также указать такой закон переключения, который осуществлял бы не только стабилизацию (вообще говоря, неустойчивой) системы, но и обеспечивал бы достаточно высокое качество регулирования. С этой целью определим закон изменения величины а следующим образом. Рассмотрим две плоскости:

Riix, у, z) = Ax-i-By-i-z = 0,) R,(x, у, z) = Ax-By-z-e{x-i-Ty) = 0, ]

где А, В, б, Т - положительные постоянные, и разобьем трехмерное фазовое пространство на четыре области. Область G] определим как область, в которой выполнено хО и одна из пар неравенств

а) /?,>0, /?2>0, Ь) /?,>0, R,0, с) RiO, /?,>0. Область Ga определим неравенствами х<0, RO, RO. Область, в которой х<0 к выполняется одна из пар неравенств

а) /?,<0, /?,<0, Ь) RiO, Ri<0, с)/?.<0, RO, обозначим через G3. Через G4, наконец, обозначим область, где х>0, /?1<0, /?2<0. На рис. 14 области Gi и G расположены над поверхностью переключения, а области G3 и О4 - под поверхностью. Полагаем далее а= - 1 в областях Ga и О4 и а = 1 в области О, являющейся объединением областей О, и О3 с той частью плоскости х = 0, в которой Ri Ri<0. Очевидно, закон изменения величины а при X ф О может быть задан формулой

а = sign [{Ri + R,) sign X + /?. - R,\]. (9.4)

Таким образом, рассматриваемая система является системой с двойным переключением.

При переходе через плоскость ;>; = 0 величина а, очевидно, меняет свой знак, если RiRO, и не меняет своего значения, если /?,/?2<;0. Поверхность переключения, изображенную на рис. 14, составленную из частей 5i и 5з