точка M{t) сойдет с плоскости s = 0 и начнет двигаться под действием уравнений системы (7.7) либо в полупространстве

sO (при а=- 1), либо в полупространстве s<0 (при а=1). Покажем, что при достаточно большом значении Л" точка M{t) системы (7.7), побывав некоторое достаточно малое время вне плоскости 5 = 0, вновь вернется в нее в точке, расположенной достаточно близко к оси Оу.

Пусть для определенности точка Мо расположена во втором квадранте плоскости 5 = 0, т. е. для ее координат выполняются соотношения - ДдгХо<0, 00 (рис. 13). Кроме того, предположим, что выполняется также соотношение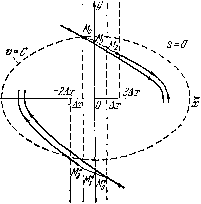

Рис. 13.

Уо>х.

Пользуясь уравнениями

У= + 9(Х У)>

dx ds

F{x, у, s-f (р(х, ;;), t) - - аКх - fxy - (рср,

(7.12)

(7.13)

полученными из дифференциальных уравнений системы (7.7), найдем приближенное решение у(х) и s{x) системы (7.13), соответствующее траектории изображающей точки M{t) с начальной точкой 7Ио(Хо, Jo) = l(o)- Так как для точки 7И„, по предположению, имеем уоО, то с ростом времени tt(, изображающая точка, сойдя с плоскости s = 0, движется в сторону возрастания х, т. е. по направлению к плоскости лг=0. С другой стороны, поскольку jCoAjc, а

величина Ах=~ может быть сделана за счет увеличения

значения К сколь угодно малой, то искомое решение будем рассматривать на интервале [х, 0], а для нахождения соответствующего решения ограничимся его первым приближением

y{x)=y, + -f{x-x,\

5 {X) = аКх, - {X - X,).

Полученные формулы позволяют найти приближенное значение координат точки Mj {х, у, s,) - точки, в которой траектория пересекает при некотором значении t=:tito плоскость jc = 0, а именно, получим равенства

х, = 0, y,=y,-lS5Xoyo, s,0, Уо

справедливые при достаточно больших значениях К, когда можно пренебречь слагаемыми одного порядка малости с величиной Ajc.

Из точки Ml изображающая точка М (t) движется с ростом времени tti в полупространстве дгО до тех пор, пока ордината точки остается положительной. Так как ордината точки Ml вследствие выполнения соотношения (7.12) снова положительна, то с ростом времени t изображающая точка Ж (О из точки Ml движется вновь в сторону возрастания x(t), по крайней мере для значений х положительных, достаточно малых, сравнимых по величине с числом Ajc. Найдем решение s{x) системы (7.13), соответствующее выходящей из точки Ml траектории, в виде степенного ряда по степеням х, пренебрегая степенями х, начиная с х. При этом примем во внимание ограниченность функций F{x,y, z, t), ср (jc, у) и их производных, а также считаем значение К достаточно большим. Тогда будем иметь

s(x)=-x~aK, (7.14)

Уо 4Уо

откуда найдем значение х, при котором функция s{x) обращается в нуль. Тем самым найдем значение абсциссы точки Mi = M{ti) - точки возвращения при = iJ, изображающей точки на плоскость s=0. Очевидно, для абсциссы

точки Mi получим равенство лг = - . Принимая

во внимание условие (7.9) получим соотношение 1 х j = 2Длг. Причем для рассматриваемой траектории, очевидно, хО, так как значение ординаты точки отличается от ординаты начальной точки траектории на величину одного порядка малости с величиной Длг, т. е. на интервале [-Длг, 2Длг] знак ординаты точки в нашем случае остается положительным.

Таким образом, мы показали, что при достаточно большом значении К изображающая точка M{t) системы (7.7), сойдя с плоскости s = 0 в точке Мо(х у), для координат которой справедливы соотношения лго Длг, у Дх, вновь возвращается на плоскость s = 0 в точке М{х, у), ордината которой по-прежнему положительна и сравнима по величине с числом Jo. 3 абсцисса не превосходит числа 2x (см. рис. 13). Поскольку разность абсцисс точек и не больше числа ЗДх, то время перехода изображающей точки из точки Жо в точку Mi при достаточно большом значении К будет малым.

Аналогичные рассуждения могут быть проведены для траектории системы (7.7), сходящей с плоскости s = 0 в некоторой точке М*(х*, у*), где у* <0 и 0<Хо Дх, если только выполняется соотношение \у*\\х, т. е. и в этом случае может быть показано, что изображающая точка M{t), покинув плоскость s = 0 в точке М*, пересечет плоскость х = 0, затем, побывав некоторое малое время вне плоскости, вновь вернется в нее в области скольжения в точке (х*, у*), для координат которой имеют место соотношения xf<0, I 2Дх.

Итак, наличие полосы х = Дх, содержащей внутри себя области прошиваемости системы (7.7), вызывает отклонение рассмотренных траекторий системы от плоскости s = 0. Это отклонение происходит на полосе, не выходящей из

полосы х2Дх. Так как Дх = , где т - постоянная

из соотношения (7.9), то всегда можно выбрать значение К настолько большим, что значение Дх станет сколь угодно малым. Одновременно с Дх станут сколь угодно малыми как максимальное отклонение функции s(x) от нуля, так и время нахождения изображающей точки рассматриваемых траекторий вне плоскости s = 0.