будут спиралевидными кривыми, а начало координат будет особой точкой типа «фокус». Если а О, то изображающая точка будет приближаться по траектории к началу координат, которое будет в этом случае асимптотически устойчивым положением равновесия (рис. 8). Если же а<0, то точки фазового пространства будут уходить от начала координат.

В областях Оз и Gj действует система (2.6); ее характеристическое уравнение имеет вид

[i-fa[x-fft -/С=0. (2.10)

При достаточно большом значении Акорни этого уравнения

будут вещественными противоположных знаков. Начало координат в данном случае будет особой точкой типа «седло». Система (2.6) будет иметь среди своих интегральных кривых две интегральные прямые, y = [i,x иу = = [>-х. Это обстоятельство может быть установлено путем простой подстановки функций y = у = [хзд: в

уравнение = - ft-

эквивалентное

Pj, 3 системе (2.6). Указанные ин-

тегральные прямые выполняют роль асимптот, к которым приближаются остальные интегральные кривые системы, имеющие гиперболический тип (рис. 9).

Отметим теперь следующий факт. Графиком функции f () = ll?-\-b - К будет парабола, пересекающая ось [х в точках = и [х = [хз (рис. 10).

Если выполнено неравенство [л [л jaj, то f(ii.)0. Пусть Л>0: полагая [л = - А[1., получим /(-А) = = - аА-\-Ь - КгО. Таким образом, второе неравенство условий (2.7) будет удовле1Ворено, если -Л[х2, т. е. если

угол между линией переключения 5 и осью х меньше угла между прямой y - Lix и той же осью.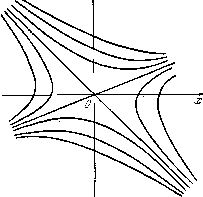

Рис. 9.

Первое из неравенств (2.7) всегда может быть удовлетворено за счет выбора достаточно большого значения К,. Таким образом, выбирая достаточно большое значение К и выбирая А согласно условию О Л - [А2> обеспечим наличие скольжения во всех точках прямой Х

Из рис. И, где приведен фазовый портрет системы (2.2), видно, что любая точка фазового пространства, двигаясь по траекториям системы (2.2), попадет на 5. Попав на 5, изображающая точка начинает совершать скольжение по этой линии к началу координат.

В- самом деле, нетрудно показать, пользуясь правилом определения вектора скорости скольжения, данным в конце

предыдущего параграфа, что дифференциальное уравнение скольжения имеет вид х-{-Ах = 0. Действительно, из этого

правила следует, что век- торы и F", выходящие

из точки М (см. рис. 7), имеют одинаковые проекции на ось Ох, равные ординате у точки М. Отсюда следует, что проекция вектора скорости

скольжения MP тоже равна у, таким образом, имеем уравнение х=у. С другой стороны абсцисса X и ордината у точки М связаны соотношением Ах-\-у = 0. Отсюда и получается требуемое дифференциальное уравнение х -{- Ах = О, из которого следует, что при Л>0 скольжение будет совершаться по направлению к началу координат по закону

Структурная схема системы, соответствующей уравнению (2.1), изображена на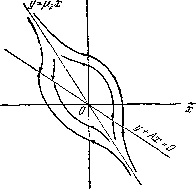

Рис.

рис. 12.

Здесь, так как рассматривается система стабилизации, соответствующая некоторой следящей системе, полагаем ф = 0 и ср == - X. Передаточная функция L (р) имеет вид L(j?)=p ар Ь. В блоке F формируется по

значениям величины >: и ее производных величина а, в блоке Л/ величина х умножается на а.

В заключение покажем, как в случае а>0 можно применить к исследованию устойчивости рассмотренной системы метод функций Ляпунова. Сначала рассмотрим функцию v =

Рис. 12.