ния изображающей точки по поверхности до тех пор, пока точка не выйдет за пределы области скольжения (участок АВ на рис. 6).

Перечисленные три группы точек на поверхности переключения отделены друг от друга в общем случае некоторыми я - 2-мерными многообразиями, в точках которых

либо

S = О, либо

lim s = 0, либо выполняют-

ся оба равенства вместе.

Остановимся более подробно на точках третьего типа. Пусть точка М лежит в области скольжения на поверхности 5. Рассмотрим векторы F~ и F", выходящие из этой точки. Концы этих векторов соединим прямой линией и найдем точку пересечения Р полученной прямой с касательной плоскостью, проведенной к поверхности 5 в точке М

(рис. 7). Всюду в дальнейшем мы будем исходить из следующей гипотезы [63]. Вектор скорости скольжения в точке М совпадает с вектором MP.

Указанное рабочее правило, подтвержденное на практике, даст нам в дальнейшем возможность выводить дифференциальные уравнения скольжения.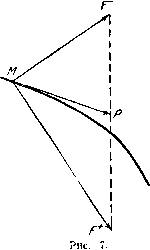

§ 2. Стабилизация системы второго порядка

Рассмотрим уравнение второго порядка

X -{-ах Ьх = ~ аКх. (2.1)

Здесь а, Ь - произвольные постоянные, К-положительная постоянная, величина а удовлетворяет условию а 1. Найдем закон изменения величины о, обеспечивающий асимптотическую устойчивость нулевого решения уравнения (2.1).

3 Е. А. Барбашии

Представив уравнение (2.1) в виде системы

X =у, р= - Ьх - ау - аКх, (2.2)

попытаемся отыскать о, исходя из следующих соображений. Пусть v{x, у)-какая-либо функция переменных х,у. Такой функцией может служить, например, потенциал некоторого векторного поля в фазовом пространстве переменных х vi у.

Подберем величину а так, чтобы обеспечить наибольшую скорость убывания функции v вдоль траекторий системы (2.2) [66,79]. Так как

dv dv , , dv

и так как от а зависит только последнее слагаемое, то minti достигается, если положить

« = signx. (2.3)

Если, например, г» = у Bx -)- Аху -]~ уто получим

a=s\gn{Ax-\-у)х. (2.4)

Итак, рассмотрим систему (2.2), считая, что величина а определяется соотношением (2.4). Система (2.2) может быть записана теперь в виде двух систем:

X =у, р = ~Ьх~ау ~ Кх, (2.5)

при X(Ах-~\-у)0, и

х=у, р = ~Ьх-ау-\-Кх, (2.6)

при х{Ах-\-у)<0.

Фазовая плоскость делится прямыми л; = О и s=:Ax-\-y = 0 на четыре части, Gj, G, G3, G4, заданные соответственно неравенствами (G,): л;> О, s>0; (G3): л:<0, s>0; (G3): x<0, s<0 и (Gi):x>0, s<0.

Линии л: = 0 и Лд;-)-у = 0 являются линиями переключения, на них совершается переход с траекторий одной системы на траектории другой системы.

Так как при л; = 0 имеем хО, если О, и х<0,, если у <0, в силу обеих систем (2.5) и (2.6), то линия л; = 0 пересекается траекториями в направлении хода часовой стрелки, т. е. все точки линии л: = О (кроме точки, гдед/ = 0) являются

точками «прошивания». Исследуем теперь точки прямой s - Ax-{-y=:0, которую в дальнейшем будем называть прямой 5. Чтобы найти условия, при выполнении которых прямая 5 будет прямой скольжения, найдем s в силу системы (2.2) на этой прямой:

-(Л -аЛ + + а/Олг-Имеем при л;0

lim 5 = (Л2 -аЛ + й + АЭлг,

lim s = ~iA--aAb - K)x,

a при л:<0

lim Ь = ~(А - аАЬ -K)x,

lim s = --(A~aAb-\-K)x.

Так как условия существования скольжения имеют вид lim ss=£0 и Нш sO,

s-.+-0 s --О

ТО они в рассматриваемом случае эквивалентны условиям

Л-2 -аЛ-f & + /С0, -аЛ + & -/С<0, (2.7)

которые можно записать в более компактной форме:

\А - аА-{-Ь\:К. (2.8)

Таким образом, условие (2.8) является необходимым и достаточным условием существорания скользящего режима у системы (2.2). Очевидно, выполнение этого условия всегда можно обеспечить за счет выбора достаточно большого значения коэффициента усиления К-

Перейдем lenepb к исследованию системы (2.2) в каждой из областей G„ г= 1, 2, 3, 4. В областях Gj и Gg имеем а= 1, здесь действует система (2.5). Характеристическое уравнение этой системы имеет вид

Х2 -ал + & + /С=0. (2.9)

При достаточно большом значении К корни этого уравнения будут комплексными, следовательно, интегральные кривые