Уравнение (1.1) можно рассматривать как дифференциальное уравнение, если символ р понимать как оператор дифференцирования.

Записав (1.1) в виде х = цф, можем сделать интуитивный вывод, что для уменьшения абсолютной величины сигнала х, т. е. для увеличения точности слежения, необходимо увеличивать параметр К, который обычно называют коэффициентом усиления системы.

2. Отметим теперь следующее обстоятельство. Следящая система, о которой шла речь, постоянно подвержена действию возмущений; эти возмущения отражаются на величине сигнала х. Допустим, новое значение х после действия возмущения равно Xi = x-(- Дх. Величина х также удовлетворяет уравнению (1.1), и мы имеем

L{j))xi = Hp)~ Кхь

так как задающее воздействие ф останется одним и тем же. Легко видеть, что для величины отклонения х, т. е. для величины Дх, получим уравнение

L{p)x = - Kx. (1.2)

Если нулевое решение уравнения (1.2) асимптотически устойчиво по Ляпуноиу, то следящая система будет работать надежно, т. е. отклонение Дх с ростом времени будет асимптотически стремиться к кулю. Таким образом, исследование следящей системы сводится к исследованию стабилизирующей системы, заданной уравнением (1.2). Для того чтобы уравнение (1.2) обладало свойством асимптотической устойчивости, необходимо и достаточно, чтобы корни уравнения L(k)-\- К = 0 имели отрицательные вещественные части.

Таким образом, обеспечение точности слежения требует выбора достаточно большого коэффициента К, а обеспечение помехоустойчивости системы ведет к требованию выполнения условий Рауза - Гурвица для полинома L{\)-\-K. Покажем, что уже для системы третьего порядка эти требования противоречивы. В самом деле, пусть L (к) = -f- аХ -f- ftX -f- с. Условия Рауза - Гурвица для полинома L(k)-\- К имеют вид c-f-AO, ftO, abc -\- К. Мы видим, что уже третье условие может нарушиться для достаточно большого значения К.

§ 1] ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ. ПОСТАНОВКА ЗАДАЧИ бЗ

Возникает вопрос: не следует ли для уничтожения указанного противоречия сделать величину К достаточно большой, но переменной по знаку? Нельзя ли выбрать такой закон изменения знака величины а (а1), чтобы уравнение

L{p)x = - аКх

обладало свойством устойчивости. В дальнейшем мы этот вопрос решим положительно. Оказывается, что следящие системы со знакопеременным а обладают тем свойством, что переходный процесс, начиная с некоторого момента времени, входит в скользящий режим, не зависящий от параметров системы и от величины К- Это ценное свойство системы, обычно называемое свойством грубости, вызывает большой интерес к системам указанного типа со стороны инженеров.

В дальнейшем все системы, работа которых основана на принципе скачкообразного изменения параметров, будем называть системами с переменной структурой.

Фундаментальные результаты по теории скользящих режимов принадлежат Ю. В. Долголенко [27], Ю. И. Неймарку [28] и И. Флюгге-Лотц [29]. На ряд преимуществ, которыми обладают системы с изменяемым коэффициентом усиления, обратил внимание в 1957 г. А. М. Летов [30].

Исследования по теории устойчивости систем с переменной структурой проводились под руководством Е. А. Б арба-шина в Свердловске [31-48] и под руководством С. В. Емельянова в Москве [49-61]. Несколько иной подход к указанным системам имеется в работе С Дж. Гаррета [62].

3. Рассмотрим теперь систему дифференциальных уравнений

~g = XiiXi.....х„), i=l, 2, п. (1.3)

Предположим, что на некоторой поверхности S, заданной уравнением s(Xi, х„) = 0, правые части системы (1.3) допускают разрывы первого рода. Это значит, что в любой точке (jcj, ..., х%) поверхности 5 для любой функции Xi (Xi,х„) существуют конечные пределы Иш Xi, Иш Xi, и эти пре-

X--1-0 X-о

делы могут не совпадать. Пусть поверхность 5 делит фазовое пространство Е системы (1.3) на две части, Е и Е. Рассмотрим вектор F с проекциями Xi, ..., Х„ и введем обозначения f+= Иш F, F= Иш F. Очевидно, векторы и F~

определены в точках поверхности 5, кроме того, имеем lim s = F*N и lim s = FN, где через N обозначен век-

X --1-0 s->. -о

тор-градиент функции s(Xi, л:„) в соответствующей точке поверхности 5.

Точки поверхности 5 можно разделить на следующие три группы [63].

К первой группе отнесем те точки поверхности 5, в которых lim s- lim sO. В этих точках векторы F~ и

s -(-0 S-- О

направлены в одну сторону от поверхности 5. Если точка фазового пространства, двигаясь по траектории системы (1.3),

попадет в точку рассматриваемого типа, то она немедленно сойдет с поверхности 5 и перейдет в другую часть пространства Е. Здесь имеет место случай «прошивания» поверхности (рис. 6, участок ВС).

Вторая группа точек поверхности 5 определяется неравенст-второй группы долж-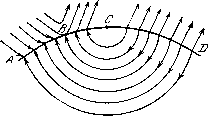

Рис. 6.

вами lim sO, lim s < 0. Точки

s -(-0 - 0

НЫ немедленно сойти с поверхности 5 по одной из траекторий системы (1.3), выходящей из данной точки (см. рис. 6, участок CD). Вопрос о том, по какой именно траектории будет совершен уход с поверхности 5, должен решаться дополнительно, так как в данном случае имеет место свойство неединственности. Часто считают, что уход будет совершаться в направлении того из векторов и F", который имеет наибольшую по абсолютной величине проекцию на нормаль N.

Наконец, точки третьего типа - это точки поверхности 5, в которых lim sO и lim sO. В этом случае траекто-

рии системы (1.3) либо втыкаются в поверхность S, либо идут вдоль этой поверхности. В случае попадания изображающей точки на поверхность 5 в конечный момент времени движение этой точки не заканчивается, начинается процесс скольже-