г л А в А II

УСТОЙЧИВОСТЬ СИСТЕМ РЕГУЛИРОВАНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ

§ 1. Предварительные замечания. Постановка задачи

В этой главе будут рассмотрены вопросы устойчивости систем автоматического регулирования с переменной структурой. В системах с переменной структурой устойчивость достигается путем скачкообразного изменения некоторых параметров системы. Характерной особенностью протекания переходного процесса в таких системах является вхождение системы, начиная с некоторого момента времени, в скользящий режим.

1. Прежде чем перейти к систематическому изложению материала, остановимся кратко на некоторых основных понятиях теории автоматического регулирования. В любой автоматической системе выделяют обычно управляемый объект и управляющее устройство или регулятор. Назначением регулятора является выработка управляющего сигнала, воздействующего на объект с целью обеспечения требуемых значений показателей регулируемого процесса. Так, например, на рис. 4 демонстрируется простейшая система регулирования уровня жидкости в баке.

Здесь регулируемой величиной является уровень h жидкости в баке. В зависимости от значения величины h в данный момент регулятор пзп-ем изменения площади сечения подающей жидкость трубы устанавливает количество жидкости х, попадающей в единицу времени в бак. По отношению к объекту, т. е. к баку, сигнал х является входным, а сигнал h - выходным сигналом. В данном случае выходной сигнал h по-ступаег в управляющее устройство с целью определения величины управляющего сигналах, таким образом, рассматриваемая автоматическая система обладает обратной связью.

В принципе автоматическая система может решать следующие задачи:

1. Поддерживать выходной сигнал объекта на одном и том же постоянном уровне (стабилизирующая автоматическая система).

2. Изменять управляемый сигнал в соответствии с заранее заданной функцией времени (программная автоматическая система).

3. Изменять управляемый сигнал в зависимости ог неизвестного заранее переменного задающего воздействия (следящая автоматическая система).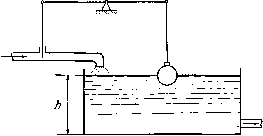

Рис. 4.

Автоматическая система может быть подразделена на звенья (объект, регулятор и т. д.), каждое из которых преобразует входной (по отношению к этому звену) сигнал х в выходной у. Математически соотношение между входной и выходной величиной может быть задано уравнением у (t) = Ах (t), где А - некоторый оператор, определенный в пространстве входных сигналов X.

Чаще всего вид оператора А определяется некоторым дифференциальным уравнением, Например, в линейном случае соотношение между y{t) и x{t) может быть задано линейным дифференциальным уравнением

P{D)y{t)=Q{D)x{t),

где Р (D), Q (D) - полиномиальные функции D,zD - оператор дифференцирования, т. е. D = .

Если исходить из нулевых начальных условий для у (t), то для изображений по Лапласу функций x{t), y{t),T. е. для функций

Х{р)] е-Р X it) dt, Y(P) = ] е-Ру {t) dt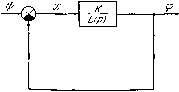

Рис. 5.

справедливо соотношение

У(р) = Щх(р).

функция Ь{р) = ущ обычно называется передаточной функцией, звена. Очевидно, передаточная функция полностью определяет вид дифференциального уравнения, описывающего данное звено. Следовательно, если дополнительно учесть начальные условия для выходного сигнала у {t), то можно, зная передаточную функцию звена, полностью определить оператор А.

Обычно автоматическую систему задают с помощью структурной схемы (блок-схемы), причем на отдельных блоках такой схемы отмечаются соответствующие передаточные функции. Так, например, на рис. 5 изображена структурная схема простейшей следящей системы.

Через ф на этой схеме обозначен задающий сигнал, через

ср - выходной сигнал. Выходной сигнал ср поступает по линии

обратной связи на вход системы, где вычитается из сигнала ф.

Сигнал х = ф - ср поступает на объект, передаточная фукнув

ция которого равна щ- Назначением следящей системы

в данном случае является отслеживание задающего сигнала ф, т. е. сигнал на выходе ср должен в результате работы системы как можно менее отличаться от сигнала ф. Таким образом, величина х должна быть возможно меньше.

Рассматривая передаточную функцию как оператор, полу-

X ср; отсюда следует, что

чаем со.отношение

L{P) L(p)x = L(j?)-

(1.1)