Заметим теперь, что если бы множество М содержало целые траектории, то из доказательства теоремы следует, что все траектории системы (12.1) притягиваются некоторым множеством, лежащим в М. Это множество является инвариантным, т. е. состоит из целых траекторий.

Последнее утверждение принадлежит Ж. Ла-Саллю [11].

Теорема 12.3 (об устойчивости в целом нулевого решения линейной системы). Если нулевое решение линейной системы асимптотически устойчиво в смысле Ляпунова, то оно устойчиво в целом.

В самом деле, нулевое решение будет асимптотически устойчивым в смысле Ляпунова только тогда, когда все корни характеристического уравнения системы имеют отрицательные вещественные части. По теореме 9.1 для любой определенно отрицательной квадратичной формы w можно указать определенно положительную форму v такую, что имеет место v = w. Так как форма v является бесконечно большой, то мы находимся в условиях применения теоремы 12.1.

§ 13. Проблема Айзермана

Наряду с линейным уравнением второго порядка

x-\-ax-bx=Q (13.1)

рассмотрим нелинейное уравнение

х + ах+/(х)=0, /(0)=0. (13.2)

Если а>0 и й>0, то нулевое решение уравнения асимптотически устойчиво в целом. Условие й > О можно трактовать как условие расположения прямой у = Ьх ь первом и третьем квадранте координатной плоскости. Возникает следующий вопрос: если график однозначной функции у = f{x) будет также расположен в первом и третьем квадранте, то будет ли нулевое решение уравнения (13.2) асимптотически устойчивым в целом? Иными словами, обеспечивают ли условия аО, f{x)хО асимптотическую устойчивость в целом, либо нужны какие-либо дополнительные условия?

Чтобы решить этот вопрос, рассмотрим функцию Ляпу-

нова v = y .\-2f{x)dx. Производная функции v в силу о

системы

X =у, р = - /(х) - ау

имеет вид v = -2ау\ Чтобы функция v была определенно положительной, необходимо потребовать выполнения условия /(х)хО. Если аО, то v будет знакоотрицательной. Очевидно, i) обращается в нуль на линии = О, не содержащей целых траекторий, кроме положения равновесия.

Таким образом, для применения теоремы 12.2 остается проследить, чтобы функция v была бесконечно большой. Для этого достаточно потребовать выполнения условия

\ f {X) dx

со

\х\-оо, либо выполнения более простого условия >s>0 при хфО.

Мы видим, что, вообще говоря, выполнения обобщенных условий Рауза-Гурвица аО, f{x)xQ недостаточно для вывода заключения о наличии свойства устойчивости в целом.

Рассмотрим теперь вопрос с более общей точки зрения. Наряду с линейной системой

dt ~

1 = 2,

(13.3)

рассмотрим нелинейную систему

¥;=2 (0)=o.

(13.4)

Пусть нам известно, что нулевое решение системы (13.3) асимптотически устойчиво для всех Ь, удовлетворяющих усло-

Будет ли нулевое решение системы (13.4) устойчивым в целом, если выполнено условие

(13.5)

Иными словами, если график кривой y-f(x) расположен между прямыми у -ах \л у - х (рис. 3), то достаточно ли этого для обеспечения устойчивости в целом нулевого реше-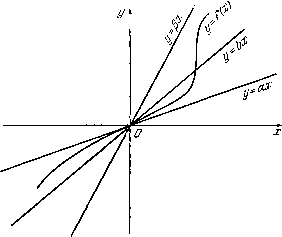

Рис. 3.

ния системы (13.4)? Эта проблема была сформулирована впервые М. А. Айзерманом [12] и явилась источником многочисленных исследований математиков и механиков.

Первый пример, показывающий, что выполнения обобщенного условия (13.5) недостаточно для наличия устойчивосги в целом, в случае системы двух уравнений построил Н. Н. Кра-совский [13].

В. А. Плисе [14] провел глубокие исследования системы третьего порядка и показал, что выполнение условия (13.5) даже в блее жесткой форме, т. е. в форме

«.<<. где «,>«, р,<р,

может не обеспечить устойчивости в целом,