тока будет зависеть от расстояния между ними:

= j.

(6.53)

Следовательно, изменение I (расстояния между электродами) позволит получить изменение плотности тока на аноде. При этом для облегчения замеров желательно, чтобы анод был плоским, а сложную форму имел катод. За исходное принимается распределение плотности тока (см. [6.45]). Поскольку такое распределение тока необходимо получить на аноде, уравнение (6.53) можно переписать для новой координатной системы так:

i{hi) =- ГЛ/г1-В/г, + С,). (6.54)

Отсюда, обозначив -£а = ак = const, получим

{Ah\-BU + C,).

Разность потенциалов между катодом сложной формы и плоским анодом поддерживается постоянной.

Для того чтобы изменялась длина анода, его делают раздвижным состоящим из двух половин - неподвижной и подвижной - электрический контакт которых осуществляется с помощью проводника. Распределение плотности тока на поверхности анода измеряется специальным устройством (рис. 6.12), состоящим из амперметра 1; трубки 2, изолирующей проводники от электро-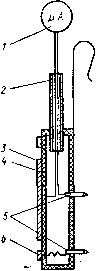

Рис. 6.12. Прибор для измерения плотности тока на аноде ванны

лита; медной пластины 5; корпуса прибора 4; двух контактных штырей 5 и экранирующего кольца 6. Контактный штырь замыкает электрическую цепь от пластины 3 через амперметр на исследуемую точку поверхности анода. Экранирующее кольцо введено для уменьшения искажения поля, вызванного толщиной прибора. На рис. 6.13, а, бив приведены экспериментальные кривые, характеризующие распределение тока для половины полоскового проводника при различной глубине деформации его края и разных углах при вершине вырыва.

Анализ этих кривых показывает, что токораспределе-ние не зависит от угла при вершине вырыва, а определяется его глубиной.

Как видно из кривых, принятое ранее предположение о стабильности тока в центре полоскового проводника {х = С) оказывается справедливым во всем диапазоне рассматриваемых деформаций края проводника.

На основании экспериментальных данных была построена кривая распределения плотности тока на краю полоскового проводника в зависимости от глубины деформации (см. рис. 6.10). На том же рисунке построена аналогичная теоретическая зависимость, полученная из (6.52). Анализ теоретических и экспериментальных кривых показывает, что при деформации полоскового проводника происходит значительное перераспределение токов в его поперечном сечении. Максимальная плотность тока имеет место на краю полоскового проводника при любой глубине деформации. Для значений С = 0,01 увеличивается плотность тока на краю полоскового проводника, в пределах 10-12% от плотности тока на краю не-деформированного проводника. При дальнейшем росте С плотность тока на краю полоскового проводника в месте его максимальной деформации уменьшается. Это наблюдается вплоть до С = 0,1. При С 0,1 плотность тока на краю деформируемого полоскового проводника возрастает и для С = 0,24 сравнивается, а для С = 0,3 на 25% превышает плотность тока на краю недеформиро-ванного полоскового проводника.

Пропускная способность полоскового волновода ограничена условиями пробоя и нагрева диэлектрика.

При работе с незатухающими колебаниями ограничивающим фактором является нагрев диэлектрика, степень которого зависит от плотности среднего тока, текущего через проводник.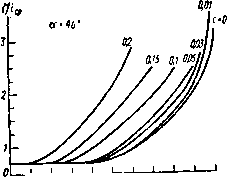

0,1 w «J e* as 0.6 0,7 as 0,9 /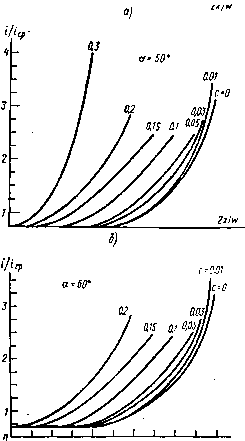

«; 0,2 0,3 0,4 0,5 0,6 op 0,8 0,9 1 e) V*v

Рис. 6.13. Распределение плотности тока в поперечном сечении полоскового проводника в зависимости от глубины дефекта края и угла при его вершине

Рост ПЛОТНОСТИ тока в деформируемом полосковом проводнике понижает допустимую плотность среднего тока. Кроме ее понижения перераспределение плотности тока по сечению проводника в результате деформации его края изменяет значения волнового сопротивления полоскового волновода в месте деформации (Zi).

По значениям Ai формулы (6.51) можно записать функции распределения тока в поперечном сечении деформируемого полоскового проводника для каждого из исследованных значений Си а по ним найти значения Zi в соответствии с выражением

A=--/j/(<:)ln-fc. (6.55)

8 = .

Результаты расчетов даны на рис. 6.14. Как видно из графика, значения Zi/Z зависят от величины С.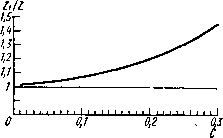

Рис. 6.14. Зависимость волнового сопротивления несимметричного полоскового волновода от глубины дефекта границы полоскового проводника

Таким образом, местные дефекты края полоскового проводника ведут к перераспределению токов в нем; это изменяет волновое сопротивление волновода в области дефекта и уменьшает допустимую плотность среднего тока, текущего в полосковом проводнике.

Если требования к полосковому волноводу такие, что перечисленные искажения недопустимы, то технологический процесс должен быть построен так, чтобы обеспечить регулярность границы проводника.

Экспериментально доказано (§ 5.1), что дефекты гра-

ницы полоскового проводника определяются толщиной и плотностью металлического осадка, подвергаемого травлению, и микрогеометрией диэлектрической поверхности, на которую нанесен металл.

Контроль толщины медных осадКов показал, что в результате неоднородности плотности тока на поверхности платы при ее гальваническом меднении появляется разброс по толщине покрытия.

Так как время травления плат выбирается применительно к вытравливанию самой толстой части покрытия, то неизбежно краевое подтравливание в областях с минимальной толщиной. Это подтверждает измерение глубины краевых дефектов: если в областях с максимальной толщиной они отсутствуют, то с уменьшением толщины покрытия глубина их растет и становится максимальной в областях минимальной толщины.

Исследования дефектов границы полоскового проводника показали, что с уменьшением величины зерна медного осадка средняя глубина дефекта также уменьшается.

ЛИТЕРАТУРА

1. Гаврилов А. Н. Технология авиационного нриборостроенпя. Оборонгиз. М., 1962.

2. Го л ант М. Б. [и др.]. Изготовление резонаторов и замедляющих систем электронных приборов, Изд-во «Сов. радио», М.,

3. Гусев В. П. Технология радиоаппаратостроения. Изд-во «Высшая школа», М., 1972.

4. Дрепберг А. Л. [и др.]. Технология неметаллических покрытий. Госхимиздат. М., 1967.

5. Иванов-Есипович Н. К. Физикохимические основы производства радиоэлектронной аппаратуры. Изд-во «Высшая школа». М., 1965.

6. Клейман Е. А. Статистические методы регулирования и контроля качества. Изд-во Комитета стандартов, мер, измерит, приборов при Совете Министров СССР. М., 1966.

7. Ковалев И. С. Теория и расчет полосковых волноводов. Изд-во «Наука и техника», Минск, 1967.

8. Л у к о м с к U й Л. Н . Теория корреляции и ее применение к анализу производства. Госэнергоиздат. М., 1958.

9. Малине кий В. Д. [и др.]. Испытания радиоаппаратуры. Изд-во «Энергия», М., 1965.

10. М а л о в А. Н. Технология холодной штамповки. Оборонгиз, М.., 1963.

11. Малорацкий Л. Г., Явич Л. Р. Проектирование и расчет СВЧ элементов па полосковых линиях. Изд-во «Сов. радпо», М., 1972.

12. Рудеико В. М. [и др.]. Малошумящие входные цепп СВЧ приемных устройств. Изд-во «Связь», М., 1971.

13. Слуцкая В. В. Тонкие пленки в технике сверхвысоких частот. Госэнергоиздат, М., 1962.

14. Ф р о л о в А. Д. Соединения в конструкциях радиотехнических изделий. Изд-во «Энергия», М., 1966.

15. Шрайбер П. Я- [и др.]. Печатные схемы в радиотехнике. Изд-во «Энергия», М., 1967,