Первый сомножитель выражает влияние регулярного, а второй - нерегулярного изменения размеров полоскового волновода. При известных выражениях для плотности вероятностей сомножителей в выражении (6.42) можно найти, во-первых, вероятность того, что при заданных регулярных изменениях ширины полоскового проводника и толщины диэлектрика значения Z лежат в требуемых границах и, во-вторых, что при заданных

нерегулярных измене-в1 ниях этих размеров

значения КСВН не превысят заданную величину. Тогда вероятность того, что Z лежит в заданных границах, будет равна произведению вероятностей для Zo и 5. Таким образом, при заданном технологическом процессе, характеризующемся определенными погрешностями, и конструкторских допусках, назначенных на размеры полоскового волновода, определяют вероятность того, что значение его полного сопротивления будет соответствовать заданным требованиям. По результатам расчетов можно судить о необходимости корректировки либо допусков на размеры, либо технологического процесса.

Оценить значения р„ можно, используя матрицу передачи участка полоскового волновода, содержащего скачок волнового сопротивления. Она представляет собой произведение нормированной волновой матрицы передачи отрезка однородной линии длиной в{ на матрицу скачка волновых сопротивлений (рис. 6.8)

Рис. 6.8. Схема скачка волнового сопротивления линии передачи

Ri-\

Ri-\ Ri+1

- 2VRi 2yJi

(6.43)

Выражения, характеризующие величину волнового сопротивления полоскового волновода в области резкого изменения его геометрических размеров, имеют вид:

--=(0,164-fiV)f

Aw \

0,836

1-f 1,735е->.<7«(

-0,826

(6.44)

Из (6.43) и (6.44) можно определить коэффициент . отражения от одной неоднородности, а зная количество неоднородностей N и их величину, нетрудно найти и рт-

§ 6.3. ВЛИЯНИЕ ДЕФЕКТОВ КРАЯ ПОЛОСКОВОГО ПРОВОДНИКА iHA ВОЛНОВОЕ СОПРОТИВЛЕНИЕ ПОЛОСКОВОГО ВОЛНОВОДА

Исследование влияния нарушений геометрии края проводника будет производиться для несимметричного полоскового волновода.

Распределение токов в полосковом проводнике имеет сложный характер. Большая часть общего тока протекает по краям проводника (рис. 6.9).

Из графика рис. 6.9 видно, что плотность тока на краях полоскового проводника более чем в три раза превышает среднюю плотность тока в проводнике. Значит, местная деформация края проводника приведет к значительному перераспределению плотности тока в нем, большему, чем для низкочастотных печатных схем. Интересен вывод аналитической зависимости плотности тока на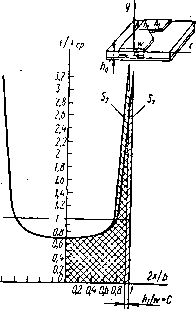

-1-dS-QS-li-l.

Рнс. 6.9. Распределение плотности тока в поперечном сечении полоскового проводника

краю проводника в месте его максимальной деформации от глубины вырыва. За исходное принимается выражение для распределения тока в полосковом проводнике

-[C-SC+C,], (6.45)

ДЛЯ 0,33 < hjw <.оо.

При выводе зависимости плотности тока на краю полоскового проводника от глубины вырыва использовались следующие допущения:

а) в деформированной части проводника изменение плотности тока по его ширине происходит по тому же закону, что и в недеформированной;

б) при деформации проводника плотность тока в его середине остается постоянной.

Для незначительных деформаций эти допущения справедливы. Решение находим из условий, что ток, протекающий в деформированной и недеформированной частях проводника, одинаков по величине, т. е. Si = S2 (см. рис. 6.9):

Я! - С2 1

-[Al~BUC,)d; (6.46) (iC*-SiC2 + C2)rfC. (6.47)

я/1-2

Для определения S используем подстановку C=sina; flfC=costflfa.

Производя интегрирование и учитывая значения постоянных, имеем при А = 0,03, В = 0,308, С, = 1,143 3 16

А-\В + ±С, = 0,Ъ.

(6.48)

Аналогично определяем, что 1

i--i-S, + C2)arcsin(l-C)-f

ib(l-C)l/2C-C4-

-jiL(i C)(4C-l-2C2)/2С-С2

(6.49)

Учитывая, что Si = S2, найдем значения Аи Bi и Cj-Для этого примем 61 = О, а С2 = С] = 1,143. Тогда

- Л1 + С2 ) arcsin (1-С)--(1-С)1/2С-С2 +

d(l С)(4С- l-2C)Y2CA=0,5. (6.50) 8

После некоторых преобразований этого выражения

8[1,57 -С2 arcsin (1 -С)]

~ 3arcsin (1 - С) + (1 - С) 1/2С С2 (4С - 5 - 2С2)

(6.51)

При этом функция, характеризующая распределение тока в полосковом проводнике, имеет вид:

ЦС) =---М,С+С)- (6.52)

я ]/ 1 - t2

В эту формулу входит Ai = f(С), т. е. она представляет собой зависимость распределения плотности тока в проводнике от глубины деформации и позволяет определить зависимость плотности тока на краю проводника от глубины деформаций. Расчет (6.51) дан в виде табл. 6.3.

Таблица 6.3

На основании (6.51) и (6.52) были произведены расчеты плотности тока на краю полоскового проводника в зависимости от глубины его деформаций, результаты которых даны на рис. 6.10.

Для экспериментальной проверки степени влияния вырывов ня перераспределение тока в полосковом проводнике можно использовать его моделирование с по-

мощью электролитической ванны, что обеспечивает точную аналогию электрического поля в любом поперечном сечении проводника и применяется для получения численных результатов, точность которых зависит только от точности проведения эксперимента.

На одном из электродов ванны создается распределение плотности тока, соответствующее распределению тока в полосковом проводнике. Затем длина этого электрода ступенями уменьшается и одновременно деформируется слой электролита введением в него диэлектриче-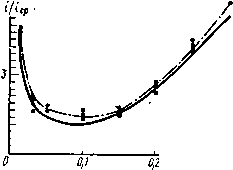

Рис. 6.10. Зависимость плотности тока на краю полоскового проводника:

- теоретическая кривая;

Z-•--экспериментальная кривая

ских клиньев, располагаемых возле деформируемого электрода (рис. 6.11). В процессе эксперимента изменяется распределение плотности тока на деформируемом электроде и общий ток, текущий через электролит. Данная модель выбирается следующим образом.

При рассмотрении модели деформированного полоскового проводника наибольший интерес представляет картина токов в плоскости поперечного сечения AAi, т. е. плоскости максимальной деформации.

Токонесущую поверхность можно смоделировать в виде некоторого проводящего слоя равномерной толщины и ширины с заданным распределением плотности тока в нем. Таким проводящим слоем в данном случае является электролит. Распределение плотности тока в любой плоскости его поперечного сечения, перпендику-

лярной к слою, остается постоянной, в том числе и на электроде, который будет условно именоваться анодом. Деформация проводящего слоя ведет к перераспределению токов в области деформации, аналогичному перераспределению в плоском проводнике, тогда, когда факторы, вызывающие первоначальное распределение токов в электролите, характерное для полоскового проводника, остаются неизменными. Это справедливо для незначительных деформаций полоскового проводника.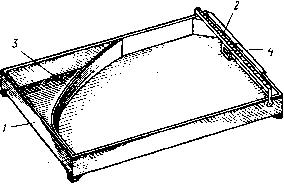

Рис. 6.11. Ванна для моделирования распределения плотности тока в поперечном сечеиии деформировай-иого полоскового проводника

Деформацию проводящего слоя можно осуществить на любом его участке и с таким расчетом, чтобьГ плоскость AAi совпала с анодом. При этом конструкция анода должна предусматривать возможность изменения его длины, а диэлектрические клинья, деформирующие электролит, надо помещать так, чтобы вершина их касалась края анода.

Электролитическая ванна для снятия рассматриваемых характеристик (рис. 6.11) состоит из прямоугольного корпуса /, плоского анода 2, катода 3, конфигурация которого рассчитывалась таким образом, чтобы получить заданное распределение тока по поверхности анода и прибора 4, измеряющего плотность тока. Форма катода рассчитывается следующим образом. Известно, что при постоянной разности потенциалов между двумя плоскими пластинами, помещенными в электролит, плотность