k2i{q2 2«*,f29 exp ( ) + ll exp

Xexp

*222 2Д*7,-г2? exp (-i + exp ()

(6.34a)

Ha рис. 6.6 показаны кривые распределения, построенные из (6.34а) в предположении, что коэффициент корреляции /? = О, а на рис. 6.7, а, б и в даны зависимости, характеризующие величину поля допуска на волновое сопротивление полоскового волновода при нулевой, десятипроцентной и двадцатипроцентной вероятности брака.

k Л Ц 51 loil ifinuTs к 41W h

Рис. 6.6. Плотность вероятности волновою сопротивления полоскового

волновода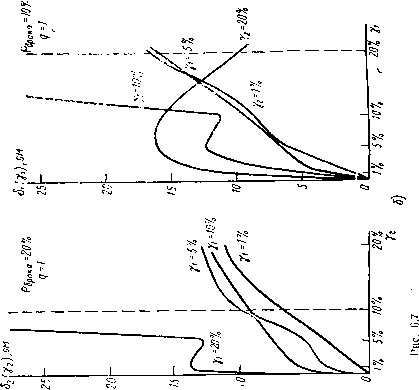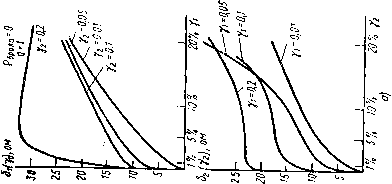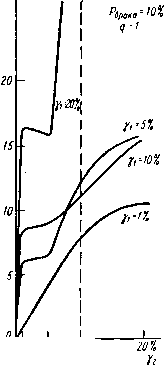

!% 5% 10%

I аха =20%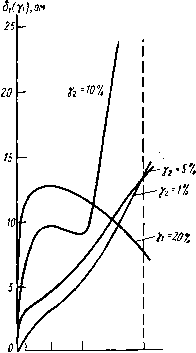

1% 5% 10%

10% ь

Нис. ь.7 (продолжение). Поле допуска 6i(yi) и С2(у2) на волноводе сопротивление Zo=50 ом полоскового волновода при вероятности брака, равной нулю (а); 10% и 20% (б> в)

С ПОМОЩЬЮ выражения плотности вероятности волнового сопротивления можно определить оптимальные значения номинальных размеров при данном процессе производства (при заданном разбросе), для которых вероятность нахождения Zo в требуемых пределах будет максимальной.

Возможно и решение обратной задачи - по допустимому разбросу определить значения допусков на to и Л, при которых вероятность попадания Zq в допуск будет заданной.

Пусть задана область допустимых значений Zq, равноценная во всех точках. Воспользовавшись выражением

для плотности вероятности Zq (6.34), можно вычислить вероятность нахождения Zo в области допустимых значений при разбросе да и /i, характерном для данного технологического процесса:

p = JjAf(Zo)flf™(/A,

(6.35)

где В - область допустимых значений w и h.

Необходимо найти такой вектор iWo(Zo)66, для которого вероятность, вычисленная из (6.35), была бы максимальной.

Поскольку область В определяется двумя независимыми переменными w и h, выражение (6.35) будет

пах ш тахЛ

р= j dw M{Z)dh.

nin w min Л

(6.36)

Для определения оптимальных номинальных значений параметров w н h возьмем частные производные этой формулы и приравняем их нулю:

max ft

Учитывая, что

dw M[Zo)dh=0;

min w min ft max w max ft

min A

(6.37)

max да -min да=/j, max Л -min A=/2.

(6.38)

подставив в (6.37) выражение (6.34), после дифференцирования и некоторых нреобразований имеем систему из двух уравнений с двумя неизвестными для определения Ада и АЛ:

802 A+lQ Y2n

"l оР + ф2

= 0;

(6.39)

а2ЛГ2+ o2q2 „2

/a?7V2 2Q2)

8ai "2

o2p2 + ,2 2 о?Я2 + ,22

Y{ValP+ ,22 ]/,2p2,2Q2 )

min A-f/j-j-ДА = /; minw-\-Aw=P;

(6.40)

Сказанное ранее справедливо тогда, когда в пределах партии полосковых волноводов имеется разброс геометрических размеров, которые строго постоянны в пределах одного волновода, т. е. для случая регулярных полосковых волноводов. Если имеется разброс и в пределах одного волновода, то возможны: колебания ширины полоскового проводника и толщины диэлектрика и сосредоточенные изменения размеров полоскового волновода. Оба вида погрешностей могут присутствовать одновременно, вызывая в полосковом волноводе отраженную волну.

Для малых неоднородностей, обусловленных разбросом, справедлив статистический подход.

Если предположить, что комплексные коэффициенты отражения по напряжению малы и аддитивны, то

где рг - коэффициент отражения от i-ой неоднородности; - количество неоднородностей. Далее предполагаем, что длины линий между неоднородностями не зависят друг от друга, а все углы в в пределах О-2я являются равновероятными и общее число неоднородностей велико. При этих допущениях и замене плавного изменения размера ступенчатым со. сколь угодно малой величиной ступенек известно, что общий коэффициент отражения имеет распределение Релея;

/ р

где Рт - наиболее вероятное значение р.

Если ро - среднеквадратичное значение р, то рт= = Руn12. Вероятность Р(р) того, что коэффициент отражения меньше р, определяется выражением

Я(р) = Г(р)р=.1 е

(6.41)

Этот результат можно выразить через КСВН следующим образом:

J 2

Р(5)=1-ехр

где 5 - коэффициент стоячей волны (КСВН).

Появление отраженной волны в полосковом волноводе Эквивалентно работе регулярного полоскового волновода на несогласованную нагрузку. Эффект малых неоднородностей на волновое сопротивление линии учитывается через полное сопротивление Z регулярного полоскового волновода с волновым сопротивлением Zq при наличии отраженной волны и коэффициенте отражения р:

-" (6.42)

• = Z„5.