чие сопротивлений металла проводников и «массивного» металла, на которые обычно ведется расчет затухания; многослойность полосковых проводников, состоящих из слоев металлов с разной проводимостью.

Технологический процесс изготовления плат полосковых волноводов заключается в металлизации одной поверхности платы и получении на другой рисунка полосковых проводников.

При получении волноводов на органическом диэлектрике с использованием электрохимической металлизации для увеличения адгезии на поверхности диэлектрика создаются микронеровности. Тот же метод используется при создании полосковых схем на СВЧ керамике, не содержащей стеклофазы, при металлизации с использованием вжигания.

Наносимые в. вакууме металлические пленки сцепляются с диэлектриком за счет химических связей окисла, который образуется между проводником и подложкой в тонком слое металла с относительно высоким удельным сопротивлением, например хрома, титана или тантала, а химические связи образуются на очень гладкой поверхности подложки. На высокоомный промежуточный слой наносится металл, образующий собственно проводник.

Таким образом, шероховатость токонесущей поверхности и многослойность полосковых проводников обусловлены требованиями процесса изготовления полосковых волноводов. Структура металла, зернистость, пористость, величина внутренних напряжений и, следовательно, удельное сопротивление зависят также и от способа и режимов металлизации.

Для количественной оценки степени влияния микро-неровностетей поверхности на величину затухания можно использовать коэффициент потерь

где kx-частотная поправка, зависящая от рабочей длины волны в волноводе,

/?а -среднеарифметическое отклонение микропрофиля; fif -условная глубина проникновения; /С -коэффициент шероховатости (отношение длины микропро-

филя к длине идеально гладкой токонесущей поверхности).

Коэффициент потерь показывает, во сколько раз увеличивается эффективная поверхность шероховатого проводника по сравнению с абсолютно гладким проводником, учитывает чистоту токонесущей поверхности и рабочую длину волны. Увеличение эффективной поверх-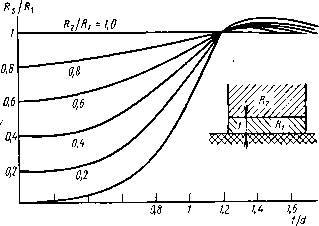

0,2 0,4 0,6

Рпс. 6.1. Зависимость поверхностного сопротивления многослойной токонесущей поверхности от сопротивления слоев, их толщины и условной глубины пронниновения

НОСТИ, без изменения линейных размеров проводников полоскового волновода, можно рассматривать как результирующее увеличение поверхностного сопротивления при абсолютно гладких токонесущих поверхностях. Значение поверхностного сопротивления токонесущих поверхностей возрастает в k раз.

Вещественная часть поверхностного сопротивления двухслойной токонесущей поверхности (рис. 6.1) определяется выражением

sin - exp 2tld d

Ы] exp(4W-2 [[f) -ij cos - exp 2./.-b - l)

,(6.1)

где Ri - удельное сопротивление поверхностной пленки; 2 - удельное сопротивление материала проводника; - толщина поверхностной высокоомной пленки металла;.d- глубина скин-слоя для материала поверхностной пленки.

Следовательно, технологический процесс влияет на величину потерь в проводниках полоскового волновода, а значит, и на величину затухания.

Величина затухания в полосковом волноводе, обусловленного потерями в проводниках при известном распределении тока

где Zo - характеристическое сопротивление полоскового волновода; /?si= (n/p,ipi)« и /?s2= (я/р-гРз)-поверхностное сопротивление в омах на квадрат для полоскового проводника и заземленных пластин соответственно; Jiix) й /2(-4)-распределение плотности поверхностного тока; / - величина общего тока, проходящего через проводник. Величины (XI, р,2, рь ра характеризуют магнитную проницаемость и удельное сопротивление материала проводника и заземленных пластин, f - рабочая частота. Множитель зависит от типа полоскового волновода. Для симметричного полоскового волновода Л=1, для несимметричного N-/2- Интеграл первого слагаемого берется по контуру проводника, второго - по поверхности заземленной пластины.

Расчет величины затухания по (6.2) затруднен ввиду сложности аналитических выражений, характеризующих распределение плотности тока в полосковом проводнике и заземленной пластине. Для определения затухания в несимметричном и симметричном полосковых волноводах используют приближенный метод, основанный на «правиле приращения индуктивности». Общее выражение для сопротивления передающей линии

(6.3)

где /?-сопротивление линии, omjm; /?s - поверхностное сопротивление, ом/м; р, - магнитная проницаемость диэлектрической среды, hjm (для немагнитных диэлектри-

КОВ р,=4я-10- н/м): dL - бесконечно малое приращение индуктивности, обусловленное бесконечно малым равномерным уменьшением размера дп всех проводников в направлении, перпендикулярном их поверхности.

Так как а- =

то из (6.3) запишем

(6.4)

Это выражение используется для вывода формул величины затухания в несимметричном и симметричном полосковых волноводах, обусловленного потерями в проводниках.

Несимметричный полосковый волновод

Для несимметричного полоскового волновода (рис. 6.2) равномерное уменьшение размеров проводников выразится так:

г-1

Рис. 6.2. Поперечное сечеиие иесимметрич-иого Полоскового волновода

= (?А - смещение поверхности заземленного проводника;

= (?Л -смещение нижней поверхности проводника; = -(да -смещение краев проводника; = -dt - смещение нижней и верхней поверхностей проводника.

Учитывая это, из (6.4) найдем:

2fio2o

dL dt

. (6.5) 271

"Т

Здесь Rsi - поверхностное сопротивление полоскового проводника; Rs2 - поверхностное сопротивление заземленной пластины.

Учитывая что коэффициенты потерь поверхностей полоскового проводника внешней (Al), внутренней (/Сг) и поверхности заземленной пластины (Кз) в общем случае не равны, то

Выражение для индуктивности следующее: (д-о Г, 8Л

(6.6)

2я L а; 32 \ Л у

. М

2 а/ J 2ft я

+0,94);

для ж) г<2; (6.7) - для да/Л > 2, (6.8)

где жда + дж); ди) = --1п+ij для да/Л < 1/2я;

ij для да г>-. (6.9)

Aw = - In -

я 1 t

Используя выражения (6.7) и (6.8) с учетом (6.9), вычислим частные производные в (6.5). Дифференцируя, получим

2/2 2ft 2h

I2h я(у + 1

dL dt

dL

2/2 2Л

2/2 2Л

\2ft П 1

+ 0,94

/да >2ft

+ 0,94

я L w j

2h\t

ft я

- + 0.94) 2A j

Для да/Л > 2

M.rj

dh 2яLl6ft2 (a()2j ft

2ft3

я l-y- + 1

- да

а» 2я

16A2 {wf

["(t-+)

2ft + < .

Для 2 > да/А >

w \2-[ 1

, 4Л У J A

dL dh

dL xo

H-o

4яда + <

Akw +1

Для да/Л <

подставляя значения производных в (6.5), имеем для да/й > 2

1 +

Я(а>/2А + 0,94)

2яе (-+0,94

[л W / я(2Л + 0 . А Л

.я(2А/< + 1)

(6.10)

для 2>у-1-А 2я